Construindo uma rede neural com uma única camada oculta usando Numpy
Implementar uma rede neural de classificação de 2 classes com uma única camada oculta usando Numpy
No post anterior , discutimos como fazer uma rede neural simples usando NumPy. Neste post, vamos falar sobre como fazer uma rede neural profunda com uma camada oculta.
- Bibliotecas de importação
Iremos importar algumas bibliotecas python básicas como numpy, matplotlib (para gráficos de plotagem), sklearn (para mineração de dados e ferramenta de análise), etc. que precisaremos.
import numpy as np
import matplotlib.pyplot as plt
de sklearn.model_selection import train_test_split
2. Conjunto de dados
Nós vamos usar o Banknote Da t Aset que envolve prever se uma determinada nota é autênticos dadas várias medidas tomadas a partir de uma fotografia. É um problema de classificação binária (2 classes). Existem 1.372 observações com 4 variáveis de entrada e 1 variável de saída. Para mais detalhes veja o link.
data = np.genfromtxt ('data_banknote_authentication.txt', delimiter = ',')
X = data [:,: 4]
y = data [:, 4]
Podemos visualizar o conjunto de dados usando um gráfico de dispersão. Podemos ver que duas classes (autênticas e não autênticas) são separáveis. Nosso objetivo é construir um modelo que se ajuste a esses dados, ou seja, queremos construir um modelo de rede neural que defina as regiões como autênticas ou não autênticas.
plt.scatter (X [:, 0], X [:, 1], alpha = 0.2,
c = y, cmap = 'viridis')
plt.xlabel ('variância da wavelet')
plt.ylabel ('skewness of wavelet ');

Agora, vamos dividir os dados em um conjunto de treinamento e um conjunto de teste. Isso pode ser feito usando a função sklearn train_test_split () . 20% dos dados são selecionados para teste e 80% para trem. Além disso, verificaremos o tamanho do conjunto de treinamento e do conjunto de teste. Isso será útil posteriormente para projetar nosso modelo de rede neural.
X_train, X_test, y_train, y_test = train_test_split (X, y, test_size = 0,2, random_state = 42)X_train = X_train.T
y_train = y_train.reshape (1, y_train.shape [0])X_test = X_test.T
y_test = y_test.reshape (1, y_test.shape [0])print ('Train X Shape:', X_train.shape)
print ('Train Y Shape:', y_train.shape)
print ('Eu tenho m =% d exemplos de treinamento!'% (X_train.shape [1]))
print ('\ nTeste forma X:', X_teste.shape)

3. Modelo de rede neural
A metodologia geral para construir uma rede neural é:
1. Defina a estrutura da rede neural (nº de unidades de entrada, nº de unidades ocultas, etc.).
2. Inicialize os parâmetros do modelo
3. Loop:
- Implementar propagação direta
- Computar perda
- Implementar propagação reversa para obter os gradientes
- Atualizar parâmetros (gradiente descendente)
Vamos construir uma rede neural com uma única camada oculta, conforme mostrado na figura a seguir:

3.1 Definir estrutura
Precisamos definir o número de unidades de entrada, o número de unidades ocultas e a camada de saída. As unidades de entrada são iguais ao número de recursos no conjunto de dados (4), a camada oculta é definida como 4 (para esse propósito), e o problema é a classificação binária, usaremos uma saída de camada única.
def define_structure (X, Y):
input_unit = X.shape [0] # tamanho da camada de entrada
hidden_unit = 4 # camada oculta de tamanho 4
output_unit = Y.shape [0] # tamanho do
retorno da camada de saída (input_unit, hidden_unit, output_unit )(input_unit, hidden_unit, output_unit) = define_structure (X_train, y_train)
print ("O tamanho da camada de entrada é: =" + str (input_unit))
print ("O tamanho da camada oculta é: =" + str (hidden_unit) ))
print ("O tamanho da camada de saída é: =" + str (output_unit))

3.2 Inicializar o parâmetro do modelo
Precisamos inicializar as matrizes de peso e vetores de polarização. O peso é inicializado aleatoriamente enquanto o bias é definido como zeros. Isso pode ser feito usando a seguinte função.
def parameters_initialization (input_unit, hidden_unit, output_unit):
np.random.seed (2)
W1 = np.random.randn (oculto_unit, input_unit) * 0,01
b1 = np.zeros ((hidden_unit, 1))
W2 = np.random. randn (output_unit, hidden_unit) * 0.01
b2 = np.zeros ((output_unit, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
parâmetros de retorno
3.3.1 Propagação direta
Para a propagação direta, dado o conjunto de recursos de entrada (X), precisamos calcular a função de ativação para cada camada. Para a camada oculta, estamos usando a função de ativação tanh :


Da mesma forma, para a camada de saída, estamos usando a função de ativação sigmóide.


Podemos usar o código a seguir para implementar a propagação direta.
def sigmóide (z):
retornar 1 / (1 + np.exp (-z))def forward_propagation (X, parâmetros):
W1 = parâmetros ['W1']
b1 = parâmetros ['b1']
W2 = parâmetros ['W2']
b2 = parâmetros ['b2']
Z1 = np.dot (W1, X) + b1
A1 = np.tanh (Z1)
Z2 = np.dot (W2, A1) + b2
A2 = sigmóide (Z2)
cache = {"Z1": Z1, "A1": A1, "Z2": Z2, " A2 ": A2}
retorna A2, cache
3.3.2 Cálculo de Custo
Vamos calcular o custo de entropia cruzada. Na seção acima, calculamos A2. Usando A2, podemos calcular o custo de entropia cruzada usando a seguinte fórmula.
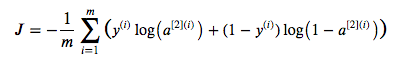
def cross_entropy_cost (A2, Y, parâmetros):
# número do exemplo de treinamento
m = Y.shape [1]
# Calcula o custo de entropia cruzada
logprobs = np.multiply (np.log (A2), Y) + np.multiply ( (1-Y), np.log (1 - A2))
custo = - np.sum (logprobs) / m
custo = float (np.squeeze (custo))
custo de retorno
3.3.3 Retropropagação
Precisamos calcular o gradiente em relação a diferentes parâmetros, conforme mostrado abaixo.

def backward_propagation (parâmetros, cache, X, Y):
# número do exemplo de treinamento
m = X.shape [1]
W1 = parâmetros ['W1']
W2 = parâmetros ['W2']
A1 = cache ['A1']
A2 = cache ['A2']
dZ2 = A2-Y
dW2 = (1 / m) * np.dot (dZ2, A1.T)
db2 = (1 / m) * np.sum (dZ2, eixo = 1, keepdims = Verdadeiro)
dZ1 = np.multiply (np.dot (W2.T, dZ2), 1 - np.power (A1, 2))
dW1 = (1 / m) * np.dot (dZ1, XT)
db1 = (1 /m)*np.sum(dZ1, axis = 1, keepdims = True)
grads = {"dW1": dW1, "db1": db1, "dW2": dW2, "db2": db2}
retornar grads
3.3.4 Gradiente descendente (parâmetros de atualização)
Precisamos atualizar os parâmetros usando a regra de descida gradiente, ou seja

onde 𝛼 é a taxa de aprendizagem e 𝜃 é o parâmetro.
def gradiente_descent (parâmetros, grads, learning_rate = 0,01):
W1 = parâmetros ['W1']
b1 = parâmetros ['b1']
W2 = parâmetros ['W2']
b2 = parâmetros ['b2']
dW1 = grads ['dW1 ']
db1 = grads [' db1 ']
dW2 = grads [' dW2 ']
db2 = grads [' db2 '] W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
parâmetros = {"W1": W1, "b1": b1, "W2": W2, " b2 ": b2}
parâmetros de retorno
4. Modelo de rede neural
Finalmente, juntando todas as funções, podemos construir um modelo de rede neural com uma única camada oculta.
def neural_network_model (X, Y, hidden_unit, num_iterations = 1000):
np.random.seed (3)
input_unit = define_structure (X, Y) [0]
output_unit = define_structure (X, Y) [2]
parameters = parameters_initialization (input_unit, unidade_oculta, unidade_saída)
W1 = parâmetros ['W1']
b1 = parâmetros ['b1']
W2 = parâmetros ['W2']
b2 = parâmetros ['b2']
para i no intervalo (0, num_iterações):
A2, cache = forward_propagation (X, parâmetros)
cost = cross_entropy_cost (A2, Y, parâmetros)
grads =backward_propagation (parameters, cache, X, Y)
parameters = gradient_descent (parameters, grads)
if i% 5 == 0:
print ("Custo após iteração% i:% f"% (i, custo)) parâmetros de retornoparâmetros = neural_network_model (X_train, y_train, 4, num_iterations = 1000)

5. Predição
Usando o parâmetro aprendido, podemos prever a classe para cada exemplo usando a propagação direta.
prediction de def (parâmetros, X):
A2, cache = forward_propagation (X, parâmetros)
predictions = np.round (A2)
retornar previsões
Se a ativação> 0,5, a previsão é 1, caso contrário, 0.
predictions = prediction (parameters, X_train)
print ('Accuracy Train:% d'% float ((np.dot (y_train, predictions.T) + np.dot (1 - y_train, 1 - predictions.T)) / float ( y_train.size) * 100) + '%')predictions = prediction (parameters, X_test)
print ('Accuracy Test:% d'% float ((np.dot (y_test, predictions.T) + np.dot (1 - y_test, 1 - predictions.T)) / float ( y_test.size) * 100) + '%')

Como podemos ver, a precisão do treinamento está em torno de 97%, o que significa que nosso modelo está funcionando e ajustou os dados de treinamento com alta probabilidade. A precisão do teste é de cerca de 96%. Dado o modelo simples e o pequeno conjunto de dados, podemos considerá-lo um bom modelo.
