Construir uma rede neural simples usando Numpy

Construir uma rede neural simples usando Numpy

Neste artigo, discutiremos como fazer uma rede neural simples usando o NumPy.

1. Bibliotecas de importação

Primeiro, importaremos todos os pacotes de que precisaremos. Precisaremos numpy , h5py (para carregar o conjunto de dados armazenado no arquivo H5) e matplotlib (para plotagem).

import numpy as np 
import matplotlib.pyplot as plt 
import h5py

2. Preparação de dados

Os dados estão disponíveis no formato (“.h5”) e contêm um conjunto de imagens de treinamento e teste rotulado como gato ou não gato. O conjunto de dados está disponível no github repo para download. Carregue o conjunto de dados usando a seguinte função:

def  load_dataset (): 
    train_dataset = h5py.File ('datasets / train_catvnoncat.h5', "r") 
    train_x = np.array (train_dataset ["train_set_x"] [:]) 
    train_y = np.array (train_dataset ["train_set_y" ] [:])test_dataset = h5py.File ('datasets / test_catvnoncat.h5', "r") 
    test_x = np.array (test_dataset ["test_set_x"] [:]) 
    test_y = np.array (test_dataset ["test_set_y"] [:])classes = np.array (test_dataset ["list_classes"] [:]) 
    
    train_y = train_y.reshape ((1, train_y.shape [0])) 
    test_y = test_y.reshape ((1, test_y.shape [0])) 
    
    retornar train_x, train_y, test_x, test_y, classes

Podemos analisar os dados observando sua forma.

train_x, train_y, test_x, test_y, classes = load_dataset ()print ("Train X shape:" + str (train_x.shape)) 
print ("Train Y shape:" + str (train_y.shape))print ("Test X shape:" + str (test_x.shape)) 
print ("Test Y shape:" + str (test_y.shape))

Temos 2 0 9 imagens de trem em que cada imagem é quadrada (altura = 64px) e (largura = 64px) e tem 3 canais (RGB). Da mesma forma, temos 50 imagens de teste da mesma dimensão.

Vamos visualizar a imagem. Você pode alterar o índice para ver imagens diferentes.

# alterar índice para outro
 índice de imagem = 2 
plt.imshow (train_x [index])

Pré-processamento de dados: o pré-processamento de dados comum para dados de imagem envolve:

1. Descubra as dimensões e formas dos dados (m_train, m_test, num_px, …)
2. Remodele os conjuntos de dados de forma que cada exemplo seja agora um vetor de tamanho (altura * largura * canal, 1)
3. “Padronizar” os dados

Primeiro, precisamos nivelar a imagem. Isso pode ser feito remodelando as imagens de forma (altura, largura, canal) em uma matriz numpy de forma (altura ∗ largura ∗ canal, 1).

train_x = train_x.reshape (train_x.shape [0], -1) .T 
test_x = test_x.reshape (test_x.shape [0], -1) .Tprint ("Train X shape:" + str (train_x.shape)) 
print ("Train Y shape:" + str (train_y.shape))print ("Test X shape:" + str (test_x.shape)) 
print ("Test Y shape:" + str (test_y.shape))

Padronizar os dados: a etapa de pré-processamento comum no aprendizado de máquina é centralizar e padronizar o conjunto de dados. Para os conjuntos de dados de imagem fornecidos, isso pode ser feito dividindo cada linha do conjunto de dados por 255 (o valor máximo de um canal de pixel).

train_x = train_x / 255. 
test_x = test_x / 255.

Agora vamos construir um modelo de rede neural simples que pode classificar corretamente as imagens como gato ou não gato.

3. Modelo de rede neural

Vamos construir uma Rede Neural conforme mostrado na figura a seguir.

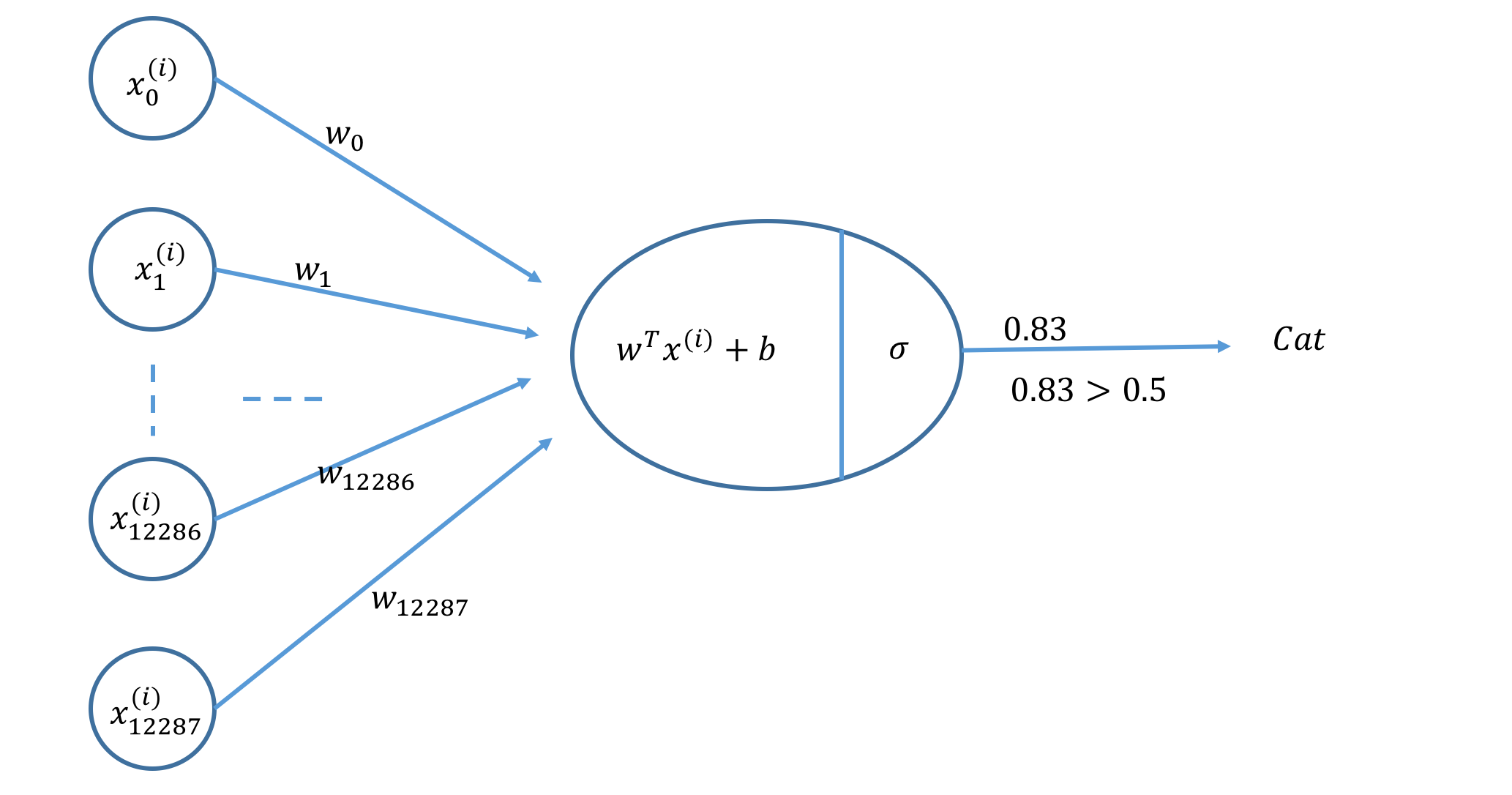
Etapas principais: as principais etapas para a construção de uma rede neural são:

1. Defina a estrutura do modelo (como número de recursos de entrada, número de saída, etc.)
2. Inicialize os parâmetros do modelo (peso e polarização)
3. Ciclo:

• Calcular a perda de corrente (propagação direta)
• Calcular gradiente atual (propagação para trás)
• Parâmetros de atualização (gradiente descendente)

3.1 Função de Ativação

A função de ativação sigmóide é dada por

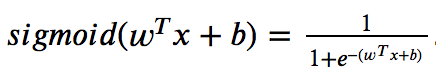
A função de ativação sigmóide pode ser calculada usando np.exp ().

def sigmóide (z): 
    retornar 1 / (1 + np.exp (-z))

3.2 Parâmetros de inicialização

Precisamos inicializar o parâmetro 𝑤 (peso) e 𝑏 (bias). No exemplo a seguir, 𝑤 é inicializado como um vetor de números aleatórios usando np.random.randn () enquanto 𝑏 é inicializado com zero.

def initialize_parameters (dim): 
    w = np.random.randn (dim, 1) * 0,01 
    b = 0 
    return w, b

3.3 Propagação para frente e para trás

Uma vez que os parâmetros são inicializados, podemos fazer as etapas de propagação “para frente” e “para trás” para aprender os parâmetros.

• Conjunto de recursos de entrada (X) são fornecidos.
• Iremos calcular a função de ativação conforme fornecido abaixo.

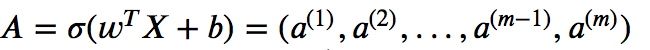
• Iremos calcular o custo conforme fornecido abaixo.

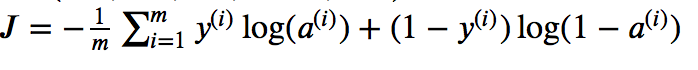
• Finalmente, calcularemos os gradientes da seguinte forma (retropropagação).

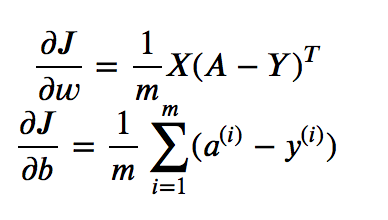
def propagar (w, b, X, Y): 
    m = X.shape [1] 
    
    #calcular função de ativação 
    A = sigmóide (np.dot (wT, X) + b)    # encontre o custo 
    custo = (-1 / m) * np.sum (Y * np.log (A) + (1 - Y) * (np.log (1 - A)))   
    #find gradiente (retropropagação) 
    dw = (1 / m) * np.dot (X, (AY) .T) 
    db = (1 / m) * np.sum (AY)    cost = np.squeeze (cost) 
    grads = {"dw": dw, 
             "db": db} 
    retornar grads, cost

3.4 Otimização

Depois de inicializar os parâmetros, calcular a função de custo e calcular gradientes, agora podemos atualizar os parâmetros usando gradiente descendente.

def gradiente_descent (w, b, X, Y, iterações, learning_rate): 
    custos = [] 
    para i no intervalo (iterações): 
        grados, custo = propagação (w, b, X, Y) 
        
        #update parâmetros 
        w = w - learning_rate * grads ["dw"] 
        b = b - learning_rate * grads ["db"] 
        costs.append (cost) 
        if i% 500 == 0: 
            print ("Cost after iteration% i:% f"% (i, cost )) 
    
    params = {"w": w, 
              "b": b}     
    return params, custos

3.5 Predição

Usando o parâmetro aprendido w e b, podemos prever os rótulos para um trem ou exemplos de teste. Para a previsão, primeiro precisamos calcular a função de ativação fornecida a seguir.

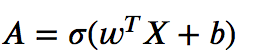
Em seguida, converta a saída (previsão) em 0 (se A <= 0,5) ou 1 (se A > 0,5) e armazene em y_pred .

def prever (w, b, X):     
    # número do exemplo 
    m = X.shape [1] 
    y_pred = np.zeros ((1, m)) 
    w = w.reshape (X.shape [0], 1) 
    
    A = sigmóide (np.dot (wT, X) + b) 
    
    para i no intervalo (A.forma [1]): 
        y_pred [0, i] = 1 se A [0, i]> 0,5, senão 0 
        passa 
    retorna y_pred

3.6 Modelo Final

Podemos juntar todos os blocos de construção na ordem certa para fazer um modelo de rede neural.

def model (train_x, train_y, test_x, test_y, iterations, learning_rate): 
    w, b = initialize_parameters (train_x.shape [0]) 
    parâmetros, custos = gradiente_descent (w, b, train_x, train_y, iterações, learning_rate) 
    
    w = parâmetros ["w"] 
    b = parâmetros ["b"] 
    
    # predizer 
    train_pred_y = prever (w, b, train_x) 
    test_pred_y = prever (w, b, test_x)    print ("Train Acc: {}%". format (100 - np.mean (np.abs (train_pred_y - train_y)) * 100)) 
    print ("Test Acc: {}%". format (100 - np.mean (np.abs (test_pred_y - test_y)) * 100)) 
    
    custos de devolução

Podemos usar o código a seguir para treinar e prever o conjunto de dados da imagem usando o modelo construído acima. Usaremos o learning_rate de 0,005 e treinaremos o modelo para 2.000 iterações .

custos = modelo (train_x, train_y, test_x, test_y, iterações = 2000, learning_rate = 0,005)

A precisão do treinamento é de cerca de 99%, o que significa que nosso modelo está funcionando e ajustou os dados de treinamento com alta probabilidade. A precisão do teste é de cerca de 70%. Dado o modelo simples e o pequeno conjunto de dados, podemos considerá-lo um bom modelo.

Finalmente, podemos traçar o custo e ver como o modelo estava aprendendo os parâmetros.

plt.plot (custos) 
plt.ylabel ('custo') 
plt.xlabel ('iterações') 
plt.title ("Taxa de aprendizagem =" + str (d ["learning_rate"])) 
plt.show ()

Podemos ver a redução do custo a cada iteração, o que mostra que os parâmetros estão sendo aprendidos.

Créditos: https://towardsdatascience.com/build-a-simple-neural-network-using-numpy-2add9aad6fc8